Design a bandpass waveguide filter

%Chebyshev BPF waveguide prototype

close all;home;clc;clear all;

%input

N=7;

Am=0.01; %ripple level in dB

R0=465;

W1=2*pi*3.3e9;

W2=2*pi*3.8e9;

W0=sqrt(W1*W2);

FBW=(W2-W1)/W0;

%================================================

beta=log(coth(Am/17.37));

gamma=sinh(beta/(2*N));

for k=1:1:N

a(k,1)=sin((2*k-1)*pi/(2*N));

b(k,1)=gamma^2+(sin(k*pi/N))^2;

end

g(1,1)=2*a(1,1)/gamma;

for k=2:1:N;

g(k,1)=(4*a(k-1,1)*a(k,1))/(b(k-1,1)*g(k-1,1));

end

g(N+1,1)=1;

for k=1:1:N;

kt=mod(k,2);

if kt==1;

CL(k,1)=1e6*(g(k,1)/FBW)*(R0/W0);%series L unit uH

CL(k,2)=1e15*(FBW/g(k,1))/(W0*R0);%series C unit fF

else

CL(k,1)=1e9*(FBW/g(k,1))*R0/W0;%series L unit nH

CL(k,2)=1e12*(g(k,1)/FBW)/(W0*R0);%series C unit pF

end

end

CL

Scaling to BPF proto type

Apply impedance inverters to LPF prototype

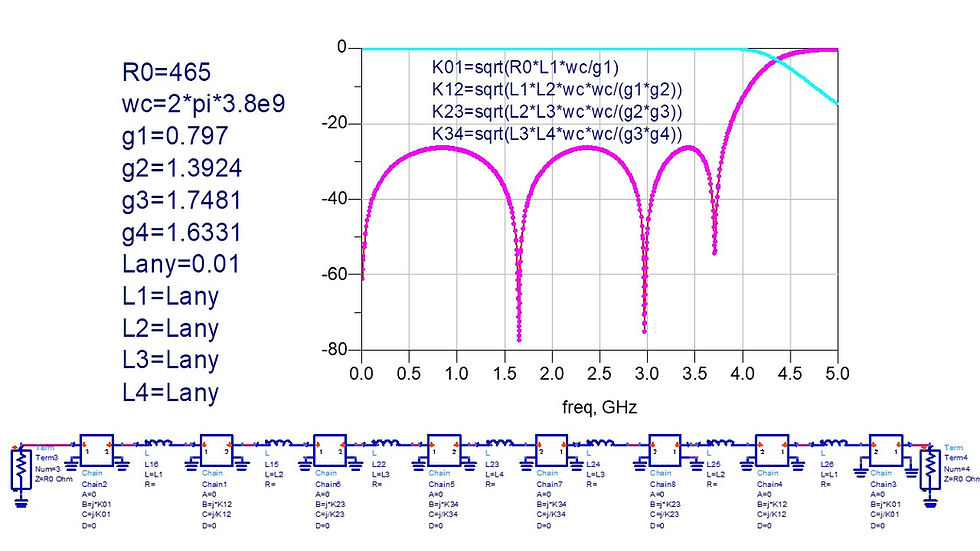
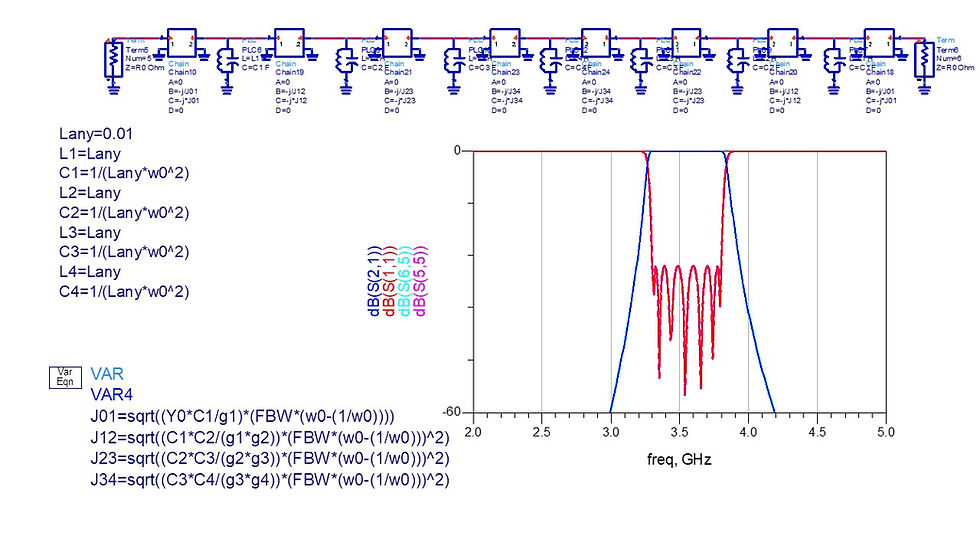
Mapping to BPF (equations) and use K inverter

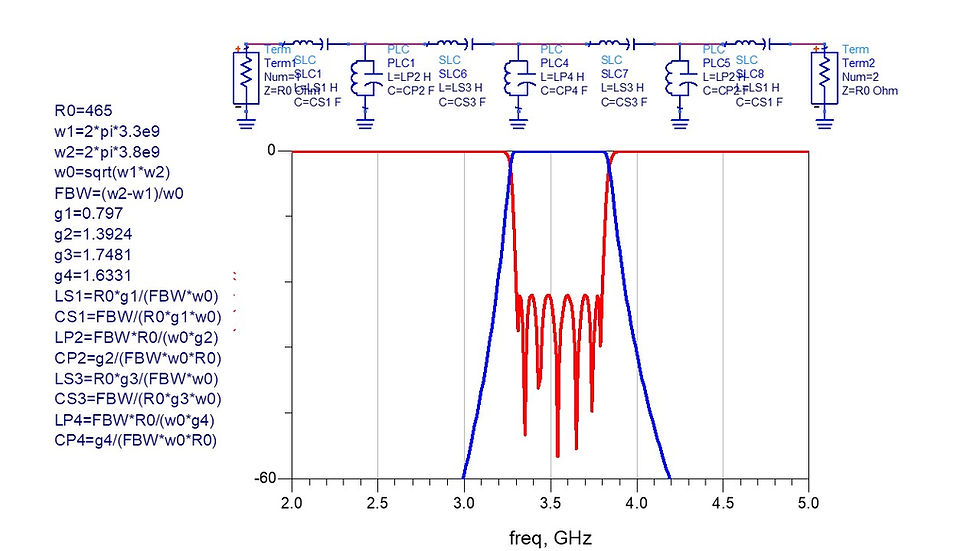
1. L and C must maintain the relationship C=1/(L*w0^2)

2. Frequency mapping exists in K inverters, using the factor (FBW*(w0-(1/w0)))^2

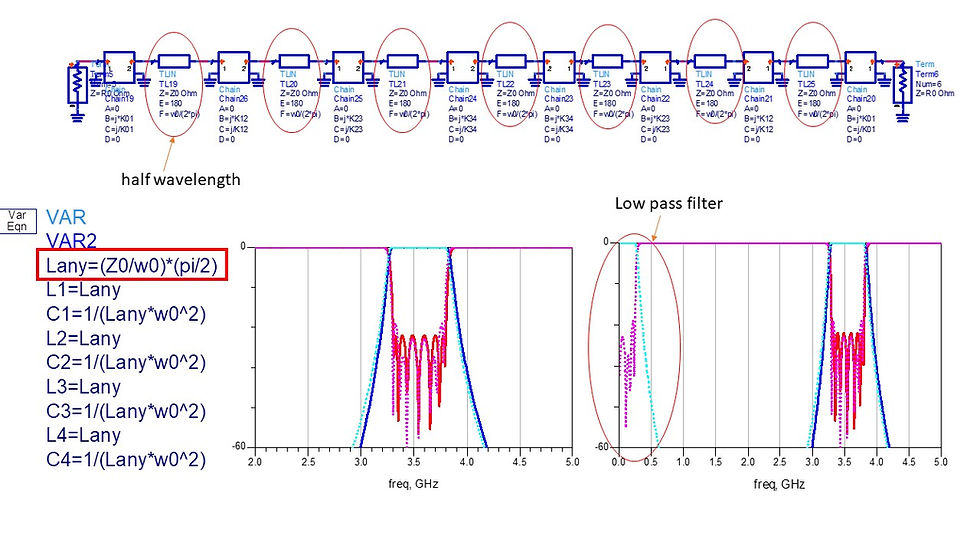
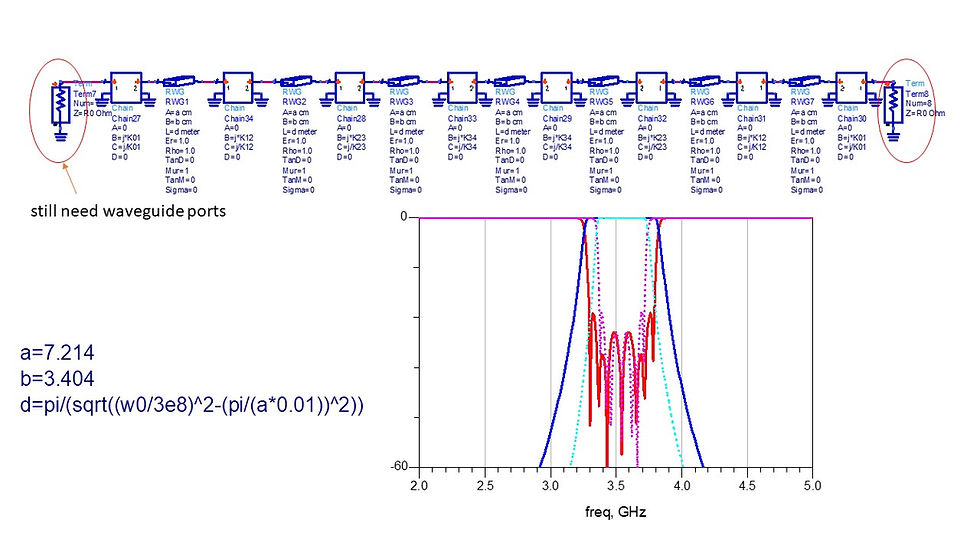
In[91]:= w1=2*\[Pi]*3.3*10^9;

w2=2*\[Pi]*3.8*10^9;

w0=\[Sqrt](w1*w2);

FBW=(w2-w1)/w0;

R0=465;

Y0=1/R0;

g1=0.797;

L1=(R0/w0)*(\[Pi]/2);

pC1=(1/(R0*w0))*(\[Pi]/2);

K01=\[Sqrt]((R0*L1/g1)*(FBW*(w0-(1/w0))))

pJ01=1/\[Sqrt]((pC1/(R0*g1))*(FBW*(w0-(1/w0))))

Out[100]= 245.298

Out[101]= 881.478

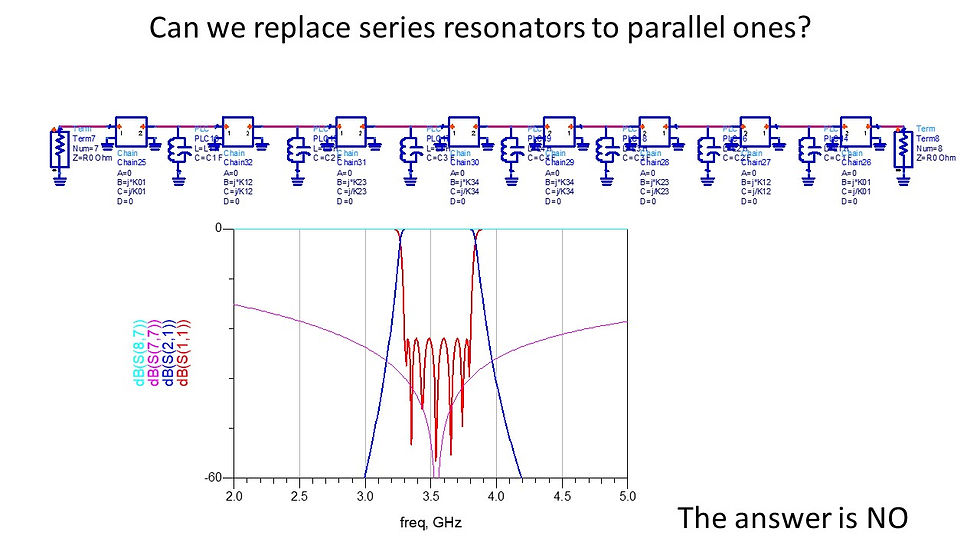
Different inverters but the same results!!